Замечание.
В этом отделе я попытался показать, каким образом выступление математического критицизма было движущей силой в поисках «оснований» математики.
Сделанное нами различие между доказательством и анализом доказательства и соответствующее различение строгости доказательства и строгости анализа доказательства, по-видимому, является решающим. Около
В начале XIX в. поток контрапримеров вызвал смущение. Так как доказательства были кристально ясными, то опровержения должны были быть занятными шалостями, должны быть полностью отделены от несомненных доказательств. Введенная Коши революция строгости базировалась на эвристическом нововведении, что математик не должен останавливаться на доказательстве: он должен пойти вперед и выяснить, что именно он доказал путем перечисления исключений, или, лучше, установления безопасной области, в пределах которой доказательство является справедливым. Но Коши — или Абель — не видели какой-либо связи между обеими задачами. Им ни когда не приходило в голову, что если они открыли исключение, то им следовало бы еще раз обратить внимание на доказательство. (Другие практиковали устранение или приспособление монстров, или даже «закрывали глаза» — но все соглашались, что доказательство представляет табу и не может иметь никакого дела с «исключениями».)
Происшедший в XIX в. союз логики и математики имел два основных источника: неевклидову геометрию и вейерштрассову революцию строгости. Этот союз привел к объединению доказательства (мысленного эксперимента) и опровержений и дал возможность развивать анализ доказательства, постепенно вводя дедуктивные формы в мысленный эксперимент доказательства. Эвристическим нововведением было то, что мы назвали «методом доказательства и опровержений»: оно впервые соединило логику и математику. Вейерштрассова строгость одержала победу над ее реакционными оппонентами с устранениями монстров и скрытыми леммами, которые пользовались лозунгами вроде «скуки от строгости», «искусственности против красоты» и т. д. Строгость анализа доказательства стала выше строгости доказательства, но большинство математиков мирилось с таким педантизмом лишь до тех пор, пока он обещал им полную достоверность.
Теория множеств Кантора, давшая еще одну жатву неожиданных опровержений «строго доказанных» теорем, обратила многих членов старой гвардии Вейерштрасса в догматиков, всегда готовых сражаться с «анархистами» при помощи устранения новых монстров или отыскания «скрытых лемм» в их теоремах, которые представляли последнее слово строгости, и в то же время карали «реакционеров» более старого типа за такие же грехи.
Затем некоторые математики поняли, что стремление к строгости анализа доказательства в методе доказательства и опровержений ведет к порочной бесконечности. Началась «интуиционистская» контрреволюция; разрушающий логико-лингвистический педантизм анализа доказательства был осужден и для доказательства были изобретены новые экстремистские стандарты строгости, математика и логика были разведены еще раз.
Логики пытались снасти это супружество и провалились на парадоксах. Гильбертова строгость превратила математику в паутину анализов доказательства и потребовала остановки их бесконечных спусков путем кристально ясной совместимости доказательств с интуиционистской метатеорией. «Обосновательный слой», область не подлежащего критике предварительного знания (Uncriticisable familiarity), переместился в мысленные эксперименты математики. (См. Lakatos, 1962, стр. 179-184.)
При каждой «революции строгости» анализ доказательства проникал, все глубже в доказательства вплоть до «обосновательного слоя» (foundational layer) хорошо знакомого основного знания (familiar background knowledge)* , где верховно правила кристально ясная интуиция, строгость доказательства, а критика изгонялась. Таким образом, различные уровни строгости отличаются только местом, где они проводят линию между строгостью анализа доказательства и строгостью доказательства, т. е. местом, где должен остановиться критицизм и должно начаться подтверждение. «Достоверность» никогда не может быть достигнута, «основания» никогда не могут быть обоснованы, но «хитрость разума» превращает всякое увеличение строгости в увеличение содержания, в цель математики. Но эта история лежит вне пределов настоящего исследования.
6. Возвращение к критике доказательства при помощи контрапримеров, которые являются локальными, но не глобальными. Проблема содержания
а) Возрастание содержания при более глубоких доказательствах
Омега. Мне нравится у Ламбды его метод доказательства и опровержений и я разделяю его веру, что как-нибудь мы сможем окончательно дойти до строгого анализа доказательства и таким образом до достоверно истинной теоремы. Но даже и так сам наш метод создает новую задачу: анализ доказательства при возрастании достоверности уменьшает содержание. Каждая новая лемма в анализе доказательства, каждое соответствующее .новое условие в теореме уменьшают область ее применения. Возрастающая строгость применяется к уменьшающемуся числу многогранников. Разве включение лемм не повторяет ошибки, которую сделал Бета в игре на безопасность? Разве мы тоже не смогли бы «отступить слишком радикально, оставляя вне стен большое количество эйлеровых многогранников»?[92] В обоих случаях мы могли бы вместе с водой выплеснуть и: ребенка. Мы должны иметь противовес против уменьшающего содержание давления строгости.
Мы уже сделали несколько шагов в этом направлении. Позвольте мне напомнить вам о двух случаях и снова исследовать их.
Один случай мы имели, когда впервые натолкнулись на локальные, но не глобальные примеры[93]. Гамма опроверг третью лемму в нашем первом анализе доказательства (именно, что «при вынимании треугольников из плоской триангулированной сети мы встречаемся только с двумя возможностями: или мы вынимаем одно ребро, или же мы вынимаем два ребра и вершину»). Он вынул треугольник из середины сети, не вынимая ни одного ребра или вершины.
Мы имели тогда две возможности[94]. Первая состояла во включении ложной леммы в теорему. Это было бы совершенно правильной процедурой по отношению к достоверности, но так нехорошо уменьшило область применения нашей теоремы, что ее можно было бы применить только к тетраэдру. Вместе с контрапримерами мы выбросили бы и все наши примеры, кроме одного.
Поэтому мы разумно приняли вторую возможность: вместо сужения области теоремы вследствие включения леммы мы расширили ее, заменив лемму, сделанную ложной, другой, не являющейся таковой. Но этот существенный образец формирования теоремы был скоро забыт, и Ламбда не позаботился о том, чтобы сформулировать его в качестве эвристического правила. Оно было бы таким:
Правило 4. Если вы имеете контрапример, являющийся локальным, но не глобальным, попробуйте исправить ваш анализ доказательства, заменив отвергнутую лемму неопровергнутой другой.
Контрапримеры первого типа (локальные, но не глобальные) могут представить нам возможность увеличивать содержание нашей теоремы, которое постоянно сокращается под давлением контрапримеров третьего типа (глобальных, но не локальных).
Гамма. Правило 4 снова выявляет слабость предложенной Альфой и теперь устраненной «анализирующей доказательства зрелой интуиции»[95]. Он составил бы список подозрительных лемм, непосредственно включил их и затем — не беспокоясь о контрапримерах — формулировал бы почти пустые теоремы.
Учитель. Омега, послушаем обещанный вами второй пример.
Омега. У Беты в анализе доказательства вторая лемма состояла в том, что все грани треугольны[96]. Это может быть опровергнуто известным числом локальных, но не глобальных контрапримеров, например при помощи куба или додекаэдра. Поэтому вы, сэр, заменили ее леммой, которая нами не опровергается, а именно, что «любая грань, рассеченная диагональным ребром, распадается на два куска». Но вместо того чтобы призвать Правило 4, вы порицали Бету за «невнимательный анализ доказательства». Вы согласитесь, что Правило 4 будет лучшим советом, чем просто «будьте внимательнее».
Бета. Вы правы, Омега, и вы также заставляете меня лучше понимать «метод лучшего сорта устранителей исключений»[97]. Они начинают с осторожного, «безопасного» анализа доказательства и, систематически применяя Правило 4, постепенно строят теорему, не высказывая никаких ложных положений. В конце концов только от темперамента зависит, приближаться ли к истине сверху при помощи всегда неверных чрезмерных утверждений или же снизу при помощи всегда верных недостаточных утверждений.
Омега. Возможно, что это правильно. Но Правило 4 можно толковать двумя способами. До сих пор мы рассматривали только первую более слабую интерпретацию: «можно легко обработать, улучшить доказательство, заменив неверную лемму слегка измененной, которую контрапример не может отвергнуть[98]; для этого нужно только «более внимательное» рассмотрение доказательства и «небольшое замечание»[99]. При этой интерпретации Правило 4 будет просто заплаткой в рамках первоначального доказательства.
В качестве альтернативы я допускаю радикальную интерпретацию: заменить лемму — или, может быть, все леммы — не только пытаясь выжать последнюю каплю содержания из данного доказательства, но, может быть, изобретая совершенно другое, более охватывающее, более глубокое доказательство.
Учитель. Например?
Омега. Я обсуждал ранее догадку Декарта — Эйлера с одним другом, который сразу же предложил следующее доказательство: вообразим, что многогранник полый и имеет поверхность, сделанную из какого-нибудь твердого материала, например картона. Ребра должны быть отчетливо раскрашены с внутренней стороны; хорошо осветим внутренность, и пусть одна из граней будет линзой обыкновенной камеры — та самая грань, из которой я могу снять фотографию, показывающую все ребра и вершины.
Сигма (в сторону). Камера в математическом доказательстве?
Омега. Таким образом, я получаю изображение плоской сети, с которой можно проделать то же самое, что и с плоской сетью вашего доказательства. Таким же образом я могу показать, что для односвязных граней V — Е + F = 1 и после добавления невидимой грани-линзы на фотографии я получаю формулу Эйлера. Основная лемма заключается в том, что у многогранника имеется такая грань, которая, будучи преобразована в линзу камеры, так фотографирует внутренность многогранника, что на пленке будут все ребра и вершины. Теперь я ввожу следующее сокращение: вместо «многогранника, имеющего одну грань, с которой можно сфотографировать всю внутренность», я буду говорить «квазивыпуклый многогранник».
Бета. Таким образом, ваша теорема будет: «Все квазивыпуклые многогранники с односвязными гранями являются эйлеровыми».
Омега. Для краткости и признания заслуги изобретателя этого частного доказательства я бы сказал: «Все многогранники Жергонна будут эйлеровыми»[100] .
Гамма. Но имеется множество простых многогранников, которые, будучи вполне эйлеровыми, имеют такие скверные выступы внутри, что у них нет грани, с которой можно было бы сфотографировать всю внутренность. Доказательство Жергонна не будет более глубоким, чем у Коши,— наоборот, доказательство Коши глубже жергоннова!
Омега. Конечно! Я полагаю, что Учитель знал о доказательстве Жергонна, обнаружил его неудовлетворительность при помощи какого-нибудь локального, но не глобального контрапримера, и заменил оптическую лемму — фотографирование — более общей топологической леммой — растягиванием. При этом он пришел к более глубокому доказательству Коши не путем «тщательного анализа доказательства», сопровождавшегося небольшим изменением, но в результате радикального нововведения, полученного воображением.
Учитель. Я принимаю ваш пример, но доказательства Жергонна я не знал. Но если вы знали, почему же нам о нем не сказали?
Омега. Потому что я непосредственно отверг его при помощи нежергонновых многогранников, которые были эйлеровыми.
Гамма. Как я только что сказал, я тоже нашел такие многогранники. Но будет ли это доводом для совершенного уничтожения этого доказательства?
Омега. Думаю, что да.
Учитель. А вы не слышали о доказательстве Лежандра? Вы и его захотите уничтожить?
Омега. Я, конечно, уничтожил бы. Оно еще менее удовлетворительно; его содержание еще беднее, чем доказательство Жергонна. Его мысленный эксперимент начинался с картографирования многогранника при помощи центральной проекции на сферу, содержавшую этот многогранник. Радиус сферы он выбирал равным 1. Он выбрал центр проекции так, чтобы сфера была полностью один и только один раз покрыта сетью сферических многоугольников. Таким образом, первой его леммой было, что такая точка существует. Второй его леммой было, что для сети на сфере, полученной из многогранника, будет V — Е + F = 2; это он нашел при помощи тривиально истинных лемм сферической тригонометрии. Точка, из которой возможна такая центральная проекция, существует только для выпуклых и немногих приличных, «почти выпуклых» многогранников — класс еще более узкий, чем «квазивыпуклых» многогранников. Но теорема - «Все многогранники Лежандра являются эйлеровыми»[101] — полностью отличается от теоремы Коши, но только к худшему. Она, «к несчастью, неполна»[102]. Она представляет «пустое усилие, предполагающее условия, от которых теорема Эйлера совершенно не зависит. Она должна быть уничтожена и нужно поискать более общих принципов»[103].
Бета. Омега прав. «Выпуклость в известной степени для эйлеровости является акцидентальной. Выпуклый многогранник может быть, например, при помощи выступа или вталкивания во внутрь одной или нескольких вершин, преобразован в невыпуклый многогранник с теми же самыми конфигурационными числами. Соотношение Эйлера соответствует чему-то более фундаментальному, чем выпуклость»[104]. И вы никогда не поймаете это вашими «почти» или «квази» пустяками.
Омега. Я думал, что учитель нашел это в топологических принципах доказательства Коши, в котором все леммы Лежандрова доказательства заменены совершенно новыми. Но тогда я натолкнулся на многогранник, отвергший даже это доказательство, которое наверняка является самым глубоким из всех до него.
Учитель. Послушаем.
Омега. Вы все помните «морского ежа» Гаммы (рис. 7). Он, конечно, не был эйлеровым. Но не все звездчатые многогранники будут неэйлеровыми. Возьмите, например, «большой звездчатый додекаэдр»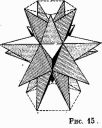 
(рис. 15). Он состоит из пентаграмм, но только иначе расположенных. Он имеет 12 граней, 30 ребер и 20 вершин, так что V — Е + F = 2[105].
Учитель. Значит, вы отбрасываете наше доказательство?
Омега. Да. Удовлетворительное доказательство должно объяснить также и эйлеровость «большого звездчатого додекаэдра».
Ро. А почему не допустить, что «большой звездчатый додекаэдр» состоит из треугольников? Ваши затруднения мнимы.
Дельта. Я соглашаюсь. Но они будут мнимыми по другой причине. Я теперь занялся звездчатыми многогранниками; они так увлекательны. Но я боюсь, что они существенно отличаются от обычных многогранников; поэтому возможно, что нельзя придумать доказательство, которое одной единственной идеей объяснило бы эйлеров характер, скажем, куба и также «большого звездчатого додекаэдра».
Омега. Почему же нет? У вас нет воображения. Стали бы вы настаивать после доказательства Жергонна и до Коши, что выпуклые и вогнутые многогранники будут существенно различными? Поэтому возможно, что нельзя придумать доказательства, которое одной единственной идеей объяснило бы Эйлеров характер выпуклых и вогнутых многогранников. Позвольте мне привести место из «Диалогов» Галилея.
«Сагредо. Как вы видите, все планеты и спутники — назовем всех их «планетами» — движутся по эллипсам.
Сальвиати. Я боюсь, что существуют планеты, движущиеся по параболам. Посмотрите на этот камень. Я бросаю его; он движется по параболе.
Симпличио. Но этот камень не планета! Это два совершенно различных явления!
Сальвиати. Конечно, этот камень будет планетой, только брошенной менее могущественной рукой, чем та, которая бросила Луну.
Симпличио. Глупости! Как вы можете соединять вместе небесные и земные явления? Одно не имеет ничего общего с другим! Конечно, оба явления могут быть объяснены доказательствами, но я, конечно, ожидаю, что оба объяснения будут совершенно различными! Я не могу вообразить доказательства, которое при помощи одной единственной идеи объяснило движение планеты в небе и ядра на Земле!
Сальвиати. Вы не можете вообразить его, а я могу придумать его»[106].
Учитель. Бросим ядра и планеты. Омега, удалось ли вам найти доказательство, которое охватило бы вместе обычные эйлеровы многогранники и эйлеровы звездчатые многогранники?
Омега. Я не нашел. Но я его найду[107].
Ламбда. Скажите, в чем же дело с доказательством Коши? Вы должны объяснить, почему отвергаете одно доказательство за другим.
