Парадокс с лифтом

Тем, кому приходится часто пользоваться лифтом, вероятно, доводилось не раз обращать внимание на один странный теоретико-вероятностный парадокс. Предположим, что лифты в этом здании ходят независимо и среднее время ожидания на каждом этаже одинаково.

Мистер Верх работает в конторе на одном из верхних этажей. Он очень удивлен. М-р Верх. Поразительно! Первым всегда приходит лифт снизу. Я замечал это неоднократно.

М-р Верх. Может быть, лифты собирают в подвале, а готовую продукцию отправляют с крыши здания на вертолетах?

Мисс Низ работает в конторе на одном из нижних этажей. Каждый день она в обеденный перерыв поднимается в ресторан, расположенный на верхнем этаже здания. Мисс Низ также очень удивлена. Мисс Низ. Ничего не понимаю! Стоит мне вызвать лифт, как он обычно приходит сверху!

Мисс Низ. Должно быть, лифты доставляют вертолетами на крышу здания, а оттуда спускают на склад в подвале.

Загадка с лифтами решается просто. По вызову мистера Верха сверху могут прийти только лифты, находящиеся в зачерненном участке шахты. Длина этого участка мала по сравнению с длиной остальной, более светлой части шахты. Следовательно, вызванный им лифт с большей вероятностью придет снизу. Так же решается и загадка, мучавшая мисс Низ.

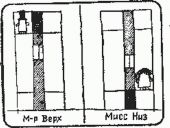
Парадокс с лифтом впервые появился в книге математических задач на смекалку, выпущенной физиком Джорджем Гамовым и его другом Марвином Стерном. Объясняя парадокс с одним лифтом, Гамов и Стерн допустили небольшую ошибку. Они утверждали, что вероятности, "разумеется, останутся такими же", если лифтов будет два или больше.

Первым, кто понял, что это не так, был известный специалист по вычислительной математике из Стэнфордского университета Дональд Кнут. В статье "Задача Гамова - Стерна о лифте" [The Journal of Recreational Mathematics, July 1969.] Кнут получил несколько неожиданный результат: с увеличением числа лифтов вероятность того, что на любом этаже (кроме первого и последнего) первым придет лифт снизу, стремится к 1/2, и вероятность того, что первым придет лифт сверху, также стремится к 1/2.

В действительности эта ситуация еще более парадоксальна, чем в первоначальном варианте задачи. Результат Кнута означает, что если вы находитесь на одном из последних этажей и стоите перед дверями одного из лифтов, то с высокой вероятностью именно тот лифт, который вы ждете, придет снизу. Если же вы готовы сесть в любой лифт, который остановится на вашем этаже, то вероятность того, что первым придет лифт снизу, будет иной. При неограниченном увеличении числа лифтов эта вероятность стремится к 1/2. То же верно и относительно лифтов, приходящих по вызову на нижние этажи сверху.

Разумеется, мы предполагаем, что лифты ходят независимо, с постоянной скоростью и что среднее время ожидания одинаково для всех этажей. Если число лифтов невелико, то вероятности изменяются незначительно. Но если число лифтов достигает 20 или более, то вероятности для всех этажей, кроме первого и последнего, мало отличаются от 1/2.

Ревнивые девушки

У одного парня были две знакомые девушки, и он никак не мог выбрать, с кем из них отправиться на свидание. Одна из девушек жила к востоку от того места, где жил он сам, другая - к западу. Ежедневно парень в случайное время спускался на станцию метро и садился в первый попавшийся поезд.

Поезда в восточном и западном направлениях шли с интервалом в 10 мин.

Девушка, жившая к востоку от того места, где обитал наш сердцеед, сказала ему как-то раз на прощание. Исти. Я так счастлива, милый, что ты навещаешь меня в среднем 9 дней из 10.

На следующий вечер девушка, жившая к западу от дома нашего героя, сердито упрекнула его. Вести. Почему ты являешься ко мне в среднем только раз в десять дней?

Необъяснимое на первый взгляд предпочтение парня к поездам восточного направления напоминает парадокс с лифтами. Хотя поезда восточного и западного направлений идут с интервалами в 10 мин, расписание составлено так, что поезд западного направления прибывает и отправляется на 1 мин позже, чем ближайший поезд восточного направления.

Чтобы попасть на поезд, идущий на запад, парень должен оказаться на станции в течение одного из минутных интервалов, отмеченных на циферблате темными полосами. Чтобы попасть на поезд, идущий на восток, он должен прибыть на станцию в течение любого из девятиминутных интервалов, заключенных между темными полосами Вероятность поехать на запад составляет 1/10, вероятность отправиться на восток составляет 9/10.

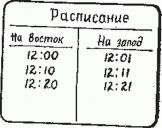
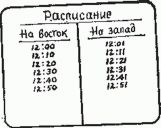
В этом парадоксе время ожидания между поездами задано расписанием. В последовательности случайных событий "среднее время ожидания" между событиями мы получим, просуммировав времена ожидания и разделив полученную сумму на п. Например, среднее время ожидания для поезда, идущего на восток, в нашем рассказе составляет 4 1/2 мин, а среднее время ожидания для поезда, идущего на запад, - всего 1/2 мин.

С временами ожидания связаны и многие другие парадоксы. Возможно, вам понравится следующий. Если вы бросаете монету, то среднее время ожидания "орла" (или "решки") равно 2 бросаниям. Это означает, что, взяв перечень исходов длинной серии бросаний монеты и подсчитав времена ожидания, отделяющие выпадение одного "орла" от выпадения следующего "орла", вы получите среднее "расстояние" между "орлами", равное 2 бросаниям (если серия начинается не с "орла", то длина серии "решек" до выпадения первого "орла" в расчет не принимается).

Предположим, что на длинном листе бумаги сверху вниз выписаны исходы длинной серии бросаний монеты. Выберите наугад зазор между двумя последовательными бросаниями (например, зажмурьте глаза и проведите по листу горизонтальную черту). Найдите ближайший к проведенной черте "орел" сверху и снизу и подсчитайте число испытаний, отделяющих один "орел" от другого. Повторите эту операцию многократно. Чему будет равно среднее расстояние между "орлами"?

Интуитивно кажется, что "орлы" должны быть в среднем разделены двумя бросаниями. В действительности в среднем их разделяют три бросания. Причина та же, по которой любвеобильный парень обычно садился в поезд, идущий на восток. Одни серии испытаний между последовательными "орлами" короткие, другие - длинные. Случайно проведенная линия аналогична случайному выбору момента прибытия парня на станцию. Попасть в более длинную серию вероятнее, чем в более короткую.

Приведем теперь простое доказательство того, что три испытания - действительно правильный ответ на вопрос задачи. Монеты "не помнят" исходов предыдущих бросаний, поэтому, где бы вы ни провели черту, среднее время ожидания до выпадения следующего "орла" должно быть равно 2 бросаниям. То же соображение применимо и к среднему времени ожидания, если мы "обратим" всю серию испытаний и будем считать времена ожидания не вперед, а назад. Следовательно, "средняя длина свободного пробега" между "орлами" равна 2x2, то есть 4, если мы будем считать и те бросания, при которых выпали сами "орлы". А так как мы условились понимать под временем ожидания длину серии испытаний, включающую выпадение следующего "орла", но не включающую выпадение предыдущего "орла", то средняя длина свободного пробега равна 4-1=3 бросаниям.

Еще более поразительна аналогичная задача с колесом рулетки. В колесе имеются 38 гнезд с номерами, среди которых есть 0 и 00. Следовательно, среднее время ожидания для любого числа, например для 7, равно 38 запускам колеса. Но если вы возьмете запись длинной серии номеров, выпавших при игре в рулетку, и, проводя наугад черту, начнете подсчитывать среднюю "длину свободного пробега" между двумя последовательными семерками, то она окажется равной не 38, а (2*38)-1=75.

Три скорлупки

Зазывала. Подходите, не робейте. Если вы правильно угадаете, под какой скорлупкой горошина, я верну вам вдвое больше денег, чем вы поставите. Поиграв немного, мистер Марк решил, что его шансы на выигрыш не превышают 1 : 3.

Зазывала. Куда же вы? Хотите, сыграем по-свойски, как друзья? Вы выбираете одну скорлупку. Выбрали? Хорошо. Теперь я переворачиваю пустую скорлупку. Горошина должна быть под одной из двух остальных. Следовательно, ваши шансы на выигрыш возрастают вдвое.

Мистер Марк легко попался на удочку. Он не понял, что от переворачивания пустой скорлупки его шансы на выигрыш не изменяются. Почему?

После того как мистер Марк выбрал скорлупку, по крайней мере одна из двух остальных скорлупок должна быть пустой. Поскольку зазывала знает, под какой скорлупкой лежит горошина, он всегда может перевернуть пустую скорлупку. Следовательно, из того, что перевернута пустая скорлупка, мистер Марк не извлекает для себя никакой полезной информации, которая позволила бы пересмотреть оценку вероятности "попадания в цель" (того, что горошина находится под выбранной им скорлупкой).

В том, что это действительно так, вы легко убедитесь, взяв туза пик и два туза красных (бубновой и червовой) мастей. Перетасовав карты, разложите их в ряд на столе вверх рубашкой. Попросите кого-нибудь выбрать одну из карт. Какова вероятность, что выбранная карта будет тузом пик? Ясно, что эта вероятность равна 1/3.

Предположим теперь, что вы заглянули в две карты, на которые не пал выбор вашего ассистента, и перевернули один из красных тузов вверх картинкой. Вы можете рассуждать следующим образом (именно так и рассуждал зазывала). Вверх рубашкой лежат только две карты. Туз пик с равной вероятностью может быть любой из них. Следовательно, вероятность того, что выбран именно туз пик, возросла до 1/2. В действительности же эта вероятность и после того, как вы перевернули красный туз вверх картинкой, осталась равной 1/3. Дело в том, что, заглянув в две оставшиеся невыбранными карты, вы всегда можете повернуть вверх картинкой именно красный туз; это ваше действие не несет никакой информации, которая могла бы повлиять на оценку вероятности угадывания туза пик.

Вы можете удивить своих друзей, показав им следующую разновидность игры в "три скорлупки". Вместо того чтобы самому заглядывать в две оставшиеся невыбранными карты и узнавать, какая из них красный туз, попросите вашего ассистента (того, кто выбрал одну из карт) перевернуть одну из двух остальных карт вверх картинкой. Если перевернутая карта окажется тузом пик, то расклад объявляется недействительным и игра повторяется до тех пор, пока перевернутая карта не окажется одним из красных тузов. Увеличивает ли подобная процедура вероятность угадать туз пик?

Как ни странно, эта процедура увеличивает вероятность угадать туз пик до 1/2. В этом мы можем убедиться, рассмотрев простой случай. Перенумеруем карты слева направо числами 1, 2 и 3. Предположим, что ваш ассистент выбрал карту 2 и перевернул вверх картинкой карту 3, которая оказалась красным тузом.

Карты при этом могут быть разложены следующими 6 способами:

Если бы третья (перевернутая) карта оказалась тузом пик, то расклад был бы объявлен недействительным. Следовательно, комбинации 4 и 6 можно исключить из рассмотрения. В четырех остальных случаях (1, 2, 3 и 5) карта 2, выбранная ассистентом, дважды оказывается тузом пик. Следовательно, вероятность того, что карта 2 - туз пик, равна 2/4=1/2.

К аналогичному результату мы пришли бы независимо от того, какую карту выберет ассистент и какая из двух остальных карт, если ее перевернуть, окажется красным тузом. Вот если бы мистеру Марку разрешалось выбрать одну из оставшихся скорлупок и она при переворачивании оказалась бы пустой, то тогда его шансы на выигрыш действительно увеличились бы с 1/3 до 1/2.

Три игральные кости

Если вам случится побывать па американской ярмарке, держитесь подальше от павильона, где всем желающим предлагают сыграть в "Чак-э-лак". Многие люди поддаются на уговоры зазывал, считая эту игру беспроигрышной.

Играют в "Чак-э-лак" следующим образом. В специальной клетке из проволоки находятся 3 игральные кости. Их встряхивают, переворачивая клетку. Игрок ставит на любое число от 1 до 6. Если названное число выпадет на одной кости, банкомет возвращает игроку ставку. Если названное число выпадет на двух или трех костях, игроку соответственно возвращают удвоенную или утроенную ставку. Игроки часто рассуждают так.

М-р Марк. Если бы в клетке была только одна кость, названное мной число выпадало бы только 1 раз из 6. Если бы в клетке было две кости, то названное число выпадало бы в 2 случаях из 6. А поскольку в клетке три игральные кости, то названное число должно выпадать в 3 случаях из 6. Шансы на выигрыш и на проигрыш равны!

М-р Марк. Но мои шансы на выигрыш еще выше! Если я поставлю 1 доллар, например, на пятерку и пятерка выпадет на двух костях, то я выиграю 2 доллара. А если пятерка выпадет на трех костях, то я выиграю 3 доллара. Игра явно должна идти в мою пользу.

Если все посетители игорных домов думают так же, как и мистер Марк, то не приходится удивляться, что владельцы игорных домов становятся миллионерами! Почему при игре "Чак-э-лак" игорный дом имеет значительно большие шансы на выигрыш, чем мистер Марк?

В "Чак-э-лак" играют во многих игорных домах в США и других странах. В Англии эта игра стала называться "Птичья клетка". Иногда в нее играют тремя костями, на гранях которых вместо точек по числу очков изображены туз бубен, туз треф, туз пик, туз червей, корона и якорь, в этом случае игру называют "Корона и якорь".

На ярмарках зазывалы обычно выкрикивают: "За один раз три выигрыша и три проигрыша!" У посетителей создается впечатление, что игра "Чак-э-лак" честная: ни одна из сторон не имеет преимущества перед другой стороной. Игра действительно была бы честной, если бы на костях всегда выпадало различное число очков. После каждого поворота клетки банкомет забирал бы 3 доллара у трех проигравших и выплачивал бы 3 доллара трем выигравшим (если на каждое число очков игроки ставят по 1 доллару). К счастью для банкомета, одно и то же число очков часто выпадает на двух или трех костях. Если одно и то же число очков выпадает на двух костях, то банкомет забирает у проигравших 4 доллара и выплачивает выигравшим 3 доллара, извлекая прибыль в 1 доллар. Если одно и то же число очков выпадает на трех костях, то банкомет забирает у проигравших 5 долларов и выплачивает выигравшему 3 доллара, извлекая прибыль в 2 доллара. Итак, числа, выпадающие одновременно на двух и трех игральных костях, составляют истинную основу благосостояния игорного дома.

Вычислить прибыль, которую приносит игорному дому игра "Чак-э-лак", по формулам - дело довольно хитрое. Проще всего составить полный список всех 216 возможных исходов бросания 3 игральных костей и убедиться, что в 120 случаях на трех костях выпадает различное число очков, в 90 случаях одно и то же число выпадает на двух костях и в 6 случаях - на трех костях. Предположим, что игорный дом провел серию из 216 партий в "Чак-э-лак", причем во всех 216 случаях исходы бросания трех костей были различными. В каждой партии 6 людей поставили по 1 доллару на каждое из 6 чисел. Следовательно, банкомет собрал ставок на общую сумму 210*6=1296 долларов. В тех случаях, когда на всех трех костях выпало различное число очков, он выплатил 120*6=720 долларов. В тех случаях, когда на двух костях выпало по одинаковому числу очков, банкомет выплатил 90*2=180 долларов тем, кто угадал число очков на третьей кости (неповторяющееся), и 90*3=270 долларов тем, кто угадал число очков, выпавшее на двух костях. Наконец, в тех случаях, когда одно и то же число очков выпало на трех костях, банкомет выплатил 6*4=24 доллара. Таким образом, всего банкомет выплатил 1194 доллара. Прибыль игорного дома составила 102 доллара, или 102/1296=1,078…, то есть более 7,8%. Это означает, что в длинной серии игр в среднем игрок теряет около 7,8 цента на каждый поставленный им доллар.

А каковы шансы на выигрыш при одном бросании? Если кости выкрашены в различные цвета, например одна в красный, другая в зеленый, а третья в синий цвета, то 1 очко на красной кости при любом числе очков на двух остальных костях может выпасть 36 различными способами. В 30 случаях число очков на красной кости отлично от 1, на зеленой кости равно 1, на синей кости - любое. Наконец, в 25 случаях число очков на красной и на зеленой костях отлично от 1, а на синей равно 1. Следовательно, в 91 случае из 216 по крайней мере на одной кости выпадает 1 очко. Следовательно, вероятность выиграть, поставив на 1 очко, составляет 91/216, то есть значительно меньше 1/2. То же самое справедливо и относительно любого другого числа очков.

Удивительные попугаи

У одной дамы было два попугая. Однажды гость спросил ее: Гость. Один из попугаев самец? Хозяйка. Да. Какова вероятность того, что оба попугая самцы? Эта вероятность равна 1/3.

Предположим, что гость спросил даму, указывая на клетку с темным попугаем: Гость. Это самец? Хозяйка. Да. На этот раз вероятность того, что оба попугая самцы повышается до 1/2. Странно! Почему вопрос, заданный о птице с темным оперением, так сильно сказывается на вероятности?

Парадокс легко решается, если выписать все возможные случаи. Если гость знает, что один из попугаев самец, то возможны три случая. Только в одном из них оба попугая самцы. Следовательно, вероятность того, что оба попугая самцы, составляет 1/3.. (Мы предполагаем, что в каждой клетке с равной вероятностью может оказаться как самец, так и самка.)

Но если гость знает, что темный попугай самец, то возможны лишь 2 случая. Только в одном из них оба попугая самцы. Следовательно, вероятность того, что оба попугая самцы, составляет 1/2.

Задачу с попугаями можно промоделировать, попросив кого-нибудь бросить 2 монеты различного достоинства и высказать некоторые утверждения относительно исходов бросаний. Бросающий может избрать одну из нескольких процедур.

1. Если выпадут два "орла", заявить: „По крайней мере одна монета выпала вверх "орлом"". Если выпадут две "решки", заявить: „По крайней мере одна монета выпала вверх "решкой"". Если одна монета выпадет вверх "орлом", а другая - вверх "решкой", заявить: "По крайней мере одна монета выпала вверх …" и дальше по своему усмотрению сказать либо "орлом", либо "решкой". Какова вероятность, что обе монеты выпали вверх той стороной, которую назвал бросающий? Ответ: 1/2.

2. Бросающий монеты заранее предупреждает, что заявит: „По крайней мере одна монета выпала вверх "орлом"" только при условии, если это действительно так. Если ни одна монета не выпадет вверх "орлом", он промолчит и бросит монеты еще раз. Какова вероятность, что обе монеты выпали вверх "орлом"? Ответ: 1/3. (На этот раз исход, когда обе монеты выпадают вверх "решками", исключается из рассмотрения, так как при таком исходе бросающий промолчит.)

3. Бросающий монеты заранее предупреждает, что объявит о том, какой стороной вверх выпадет монета меньшего достоинства, независимо от того, будет ли это "орел" или "решка". Какова вероятность того, что обе монеты выпадут вверх одной и той же стороной? Ответ: 1/2.

4. Бросающий монеты заранее предупреждает, что заявит: „По крайней мере одна монета выпала вверх "орлом"" только в том случае, если вверх "орлом" выпадет монета меньшего достоинства. Какова вероятность того, что обе монеты выпали вверх "орлами"? Ответ: 1/2.

Иногда парадокс с попугаями излагают в форме, не позволяющей решить его однозначно. Представьте себе, вы встретили незнакомца, заявившего: "У меня двое детей. По крайней мере один мальчик". Какова вероятность, что у незнакомца два сына?

Эта задача поставлена неточно: вы остаетесь в неведении относительно обстоятельств, побудивших незнакомца сделать заявление. С такой же вероятностью он мог бы, например, сообщить вам: "По крайней мере одна девочка", выбрав наугад девочку или мальчика, если у него сын и дочь, или назвав пол одного из детей, если у него два сына или две дочери. При этих условиях вероятность того, что у незнакомца два сына, равна 1/2. Подобная ситуация соответствует первой из четырех перечисленных нами процедур.

В парадоксе с попугаями неоднозначность устраняется тем, что гость задает вопрос. Первый вопрос ("По крайней мере один из попугаев самец?") соответствует второй из четырех приведенных выше процедур. Второй вопрос ("Темный попугай самец?") соответствует четвертой процедуре.

С парадоксом о двух попугаях тесно связан еще более удивительный парадокс, известный под названием "парадокс второго туза". Предположим, что вы играете в бридж. Взглянув после раздачи в свои карты, вы заявляете: "У меня туз". Какова вероятность, что у вас есть второй туз? Ответ: 5359/14498, что меньше 1/2.

Предположим теперь, что всех партнеров интересует какой-то определенный туз, например, туз пик. Игра продолжается до тех пор, пока после очередной раздачи карт вы не заявите: "Туз пик у меня". Какова вероятность того, что у вас есть второй туз? Ответ: 11636/20825, что чуть больше 1/2! Почему выбор определенного туза так изменяет шансы?

Вычисление вероятностей для всей колоды громоздко и утомительно, но суть парадокса легко понять, если воспользоваться "мини-колодой" из четырех карт, например из туза пик, туза червей, двойки треф и валета бубен. (Упрощение задачи за счет уменьшения числа элементов рассматриваемого множества нередко позволяет легко разобраться в структуре проблемы.) Колоду из четырех карт перетасуем и раздадим двум игрокам. Существует всего 6 равновероятных вариантов взяток (по 2 карты в каждой)-см. рисунок на стр. 139.

В 5 из 6 случаев игрок может заявить: "У меня туз", но второй туз у него будет лишь в одном случае из 5. Следовательно, вероятность того, что у игрока имеется второй туз, равна 1/5.

В трех случаях игрок может заявить: "У меня туз пик". Лишь в одном из этих трех случаев у него имеется второй туз. Следовательно, вероятность того, что у игрока есть второй туз, равна 1/3. Заметим, что партнеры должны заранее условиться, какой масти туз их интересует, а также о том, кто будет объявлять, если ему попадется избранный туз. Без этих оговорок задача может стать неопределенной.

• 1
• 2
• 3

• ← предыдущая
• целиком
• следующая →