Время

Парадоксы о движении, сверхзадачах, путешествиях во времени и обращении, времени

От мельчайших субатомных частиц до гигантских галактик паша Вселенная находится в состоянии непрестанного изменения; ее чудесная мозаика каждую микросекунду трансформируется в неумолимом "потоке" времени. (Слово "поток" я взял в кавычки потому, что в действительности течет Вселенная. Утверждать, будто время течет, так же бессмысленно, как утверждать, что длина простирается.)

Трудно представить себе реальный мир без времени. Объект, существующий лишь в течение нулевого времени (0 секунд), не существовал бы вообще. Или существовал бы. Во всяком случае, течение Вселенной достаточно равномерно для того, чтобы мы могли производить измерения, а измерения порождают числа и уравнения. Можно считать, что время не входит в чистую математику, но в прикладной математике от элементарной алгебры до математического анализа и далеко за его пределами имеется немало проблем, в которые время входит как фундаментальная переменная.

В этой главе собрано множество известных парадоксов о времени и движении. Некоторые из них, например парадоксы Зенона, оживленно обсуждались еще древними греками. Другие парадоксы, такие, как "замедление" времени в теории относи-кости и так называемые "машины бесконечности", способны решать "сверхзадачи". Все они еще больше разохотят вас к парадоксам и к математике.

Упомянем лишь о некоторые связях, ведущих прямиком от собранных в этой главе парадоксов к серьезной математике и науке.

Парадокс с велосипедным колесом знакомит вас с циклоидой и служит великолепным введением в геометрию кривых, более сложных, чем конические сечения. История о разочаровании, постигшем лыжника, дает наглядное представление о мощи методов элементарной алгебры, позволяющей доказать неожиданный результат. Парадоксы Зенона о резиновом канате, сверхзадачах и собаке, бегающей от одного хозяина к другому, знакомят с понятием предела, весьма существенным для понимания дифференциального и интегрального исчисления и всей высшей математики. Решение этих парадоксов связано с теорией бесконечных множеств Георга Кантора, с которой мы уже встречались в главе 2. Задача о червяке, ползущем по резиновому канату, решается с помощью знаменитого так называемого гармонического ряда. Парадоксы о времени, идущем назад, тахионах и путешествиях во времени затрагивают фундаментальные понятия теории относительности. Трюк, позволяющий избегать путешествий во времени с помощью разветвляющихся путей и параллельных миров, познакомит вас с необычным подходом к квантовой механике, известным под названием "подход многих миров".

Заключительный парадокс о конфликте между детерминизмом и индетерминизмом позволяет читателю бросить беглый взгляд на одну из извечных и наиболее глубоких проблем философии.

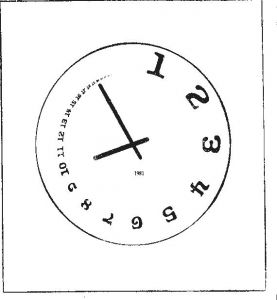
"Сумасшедшие" часы Льюиса Кэрролла

Какие часы точнее показывают время: те, которые отстают за сутки на 1 мин, или те, которые совсем не идут?

Льюис Кэрролл рассуждал следующим образом. Кэрролл. Часы, отстающие на 1 минуту в сутки, показывают точное время раз в 2 года. Часы, которые совсем не идут, показывают точное время дважды в сутки. Вы согласны? Алиса задумалась.

Алиса. Я знаю, что остановившиеся часы показывают точное время ровно в 8 часов утра и ровно в 8 часов вечера, но как узнать, когда именно наступает ровно 8 часов утра или ровно 8 часов вечера?

Кэрролл. Очень просто, дитя мое. Встань лицом к циферблату остановившихся часов и возьми в руки заряженный пистолет.

Кэрролл. Не своди глаз со стрелок часов. И в тот момент, когда часы покажут точное время, выстрели из пистолета. Всякий, кто услышит твой выстрел, будет знать, что наступило ровно 8 часов.

Льюис Кэрролл - псевдоним скромного преподавателя математики из колледжа Крайст Черч в Оксфорде Чарлза Лютвиджа Доджсона. Ему принадлежит заметка "Какие часы лучше?" о "сумасшедших" часах [Kэрролл Л. История с узелками.-М.: Мир, 1973, с.387.].

Каким образом Кэрролл определил, как часто часы, отстающие ежесуточно на 1 мин, показывают точное время? Поскольку часы каждые сутки отстают на 1 мин, они покажут точное время, когда отстанут на 12 часов, то есть через 720 суток.

Загадочное колесе

Парадокс Льюиса Кэрролла с часами - не более чем шутка, выдержанная в лучших традициях английского нонсенса. А вот "серьезный" парадокс, заслуживающий самого пристального внимания. Знаете ли вы, что верхняя часть велосипедного колеса движется быстрее, чем нижняя?

Именно поэтому спицы в верхней половине катящегося велосипедного колеса сливаются в сплошной блестящий диск.

Взгляните на два последовательных положения колеса. Точка А вблизи вершины проделала гораздо больший путь, чем точка B вблизи основания. Скорость - это расстояние, проходимое в единицу времени. Следовательно, точка A движется быстрее точки B. Верно?

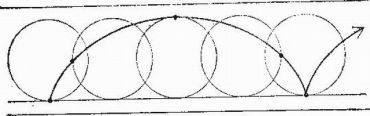
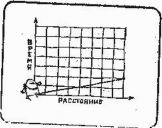
О каких скоростях идет речь, когда говорят, что верхняя часть катящегося колеса движется быстрее нижней? Разумеется, о скоростях относительно земли. Парадокс легко решается, если рассмотреть кривую, известную под названием "циклоида". Любая точка на ободе колеса, катящегося по прямой, описывает циклоиду. В точке касания колеса с поверхностью земли скорость равна нулю. Оторвавшись от земли при качении колеса, точка на ободе начинает разгоняться и в верхней точке движется с максимальной скоростью. Затем по мере приближения к земле движение точки на ободе замедляется, и в новую точку касания она приходит с нулевой скоростью. На колесах железнодорожных вагонов имеются выступы - реборды. Когда колесо катится по рельсу, точка на ободе реборды, описывая небольшую петлю, расположенную ниже уровня рельса, какое-то время движется назад.

Циклоида обладает множеством красивых математических и механических свойств. Одна из глав моей "Шестой книги математических забав" из журнала Scientific American называется "Циклоида - Елена Прекрасная геометрии". В ней, в частности, рассказывается, как начертить циклоиду с помощью катящейся банки из-под кофе. Построим циклоиду и выведя ее уравнение, вы сможете лучше оценить изящество этой кривой и ее необычные свойства.

Разочарованный лыжник

Лыжник. Какой великолепный день! Вот если бы только скорость подъемника была больше 5 км/ч! Предположим, что лыжник захочет поднять среднюю скорость, развиваемую на подъеме и спуске, до 10 км/ч. С какой скоростью он должен съезжать с горы?

15 км/ч? 60 км/ч? 100 км/ч? Хотя в это трудно поверить, но единственный способ поднять среднюю скорость до 10 км/ч для лыжника состоит в том, чтобы съехать за нулевое время!

Сначала кажется, что решение парадокса как-то связано с расстоянием, проходимым лыжником при подъеме и спуске. Но в действительности оно несущественно. Лыжник преодолевает какое-то расстояние, поднимаясь на гору, и хотел бы спуститься со скоростью, при которой средняя скорость при подъеме и спуске была бы вдвое больше скорости при подъеме. Чтобы развить такую среднюю скорость, лыжнику пришлось бы преодолеть вдвое большее расстояние (туда и обратно), чем он преодолел при подъеме, за то же время, которое он затратил на подъем. Следовательно, на спуск у нашего лыжника просто нет времени; он должен был бы преодолеть склон за нулевое время! Поскольку это невозможно, лыжник никаким способом не может поднять свою среднюю скорость с 5 до 10 км/ч, в чем вы без труда можете убедиться с помощью несложных вычислений.

Парадоксы Зенона

Древние греки придумали множество парадоксов о времени и о движении. Парадокс Зенона о бегуне ("стадий") принадлежит к числу наиболее известных.

Бегун в парадоксе Зенона рассуждал следующим образом. Бегун. Прежде чем я добегу до финиша, мне необходимо пробежать половину дистанции, затем половину оставшейся половины, то есть 3/4 всей дистанции.

Бегун. Прежде чем я преодолею последнюю четверть дистанции, мне необходимо пробежать ее половину. И так всякий раз! Прежде чем преодолеть какое-то расстояние, мне необходимо пробежать половину его. Этим половинам не будет конца! Я никогда не доберусь до финиша!

Предположим, что на преодоление половины каждого расстояния бегун затрачивает 1 мин. На графике зависимости времени от пути видно, что бегун приближается к финишу, но так и не достигает его. Правильны ли рассуждения бегуна?

Нет, неправильны: бегун не затрачивает по 1 мин на преодоление половины каждого отрезка. Каждую половину очередного отрезка он пробегает за вдвое меньшее время, чем половину предыдущего отрезка. Бегун достигнет финиша через 2 мин после старта, хотя ему придется за эти 2 мин преодолеть бесконечно много половин соответствующих отрезков дистанции.

Зенону принадлежит и другой, не менее знаменитый парадокс об Ахилле и черепахе. Быстроногий Ахилл хочет поймать черепаху, которая находится на расстоянии 1 км от него.

К тому времени, когда Ахилл добегает до того места, где первоначально находилась черепаха, та успевает уползти вперед на 10 м.

За то время, которое требуется Ахиллу, чтобы пробежать эти 10 м, черепаха снова успевает уползти на какое-то расстояние. Черепаха. Где тебе догнать меня, старина! Каждый раз, когда ты добежишь до того места, где я была, я успею уползти на какое-то расстояние вперед, хоть на толщину волоса!

Зенон, разумеется, знал, что Ахилл мог бы поймать черепаху. Свои парадоксы Зенон придумал для того, чтобы показать, к каким парадоксальным следствиям приводит представление о неделимых - "атомах" - пространства и времени, имеющих сколь угодно малые, по конечные размеры.

В обоих парадоксах Зенона бегунов следует считать точками, движущимися с постоянной скоростью вдоль прямой. Зенон знал, что если отрезок AB имеет конечную длину, то точка, движущаяся из A в B с конечной скоростью, достигает финиша за конечное время. Свои парадоксы Зенон придумал для того, чтобы продемонстрировать, к каким трудностям приводят атомистические представления о структуре пространства и времени, согласно которым отрезок "рассыпается" на отдельные неделимые элементарные отрезки, нанизанные один за другим, наподобие бусин, а время - на отдельные неделимые промежутки (и элементарным отрезкам, и элементарным промежуткам времени атомисты приписывали конечную протяженность) .

Доказать, что бегун достигнет финиша (точки B) за конечное время, поскольку на преодоление половины очередного отрезка дистанции ему потребуется вдвое меньше времени, чем на преодоление половины предыдущего отрезка (как это сделали мы), еще не означает решить парадоксы Зенона. Услышав о нашем решении, Зенон возразил бы, что, подобно тому как, прежде чем преодолеть любое расстояние, бегун сначала должен преодолеть половину этого расстояния, прежде чем истечет какой-то промежуток времени, должен истечь вдвое меньший промежуток времени. Иначе говоря, все, что Зенон говорит о прямой, в равной мере применимо и к временной последовательности событий. Время, затрачиваемое бегуном на преодоление дистанции, будет все более приближаться к 2 мин, но до истечения 2 мин всегда будет оставаться бесконечное число мгновений ("неделимых" по терминологии атомистов). То же относится и к парадоксу об Ахилле и черепахе. На каждом этапе бесконечного процесса преследования черепахи быстроногим Ахиллом впереди - и в пространстве, и во времени - неизменно будет оставаться бесконечно много "следующих" этапов.

Многие специалисты согласились со знаменитым анализом парадоксов Зенона, данным Бертраном Расселом. По мнению Рассела, парадоксы Зенона не были удовлетворительно решены вплоть до появления теории бесконечных множеств Георга Кантора.

Теория Кантора позволяет рассматривать бесконечные множества (будь то множества точек на прямой или мгновений времени) не как набор изолированных индивидуальных точек и событий, а как нечто целое. Суть парадоксов Зенона и состоит как раз Б том, что ни пространственные отрезки, ни временные промежутки недопустимо рассматривать как состоящие из бесконечно большого числа дискретных членов, изолированных друг от друга, как следы на снегу. Решение парадоксов Зенона требует теории типа канторовской теории множеств, в которой наши интуитивные представления об отдельных точках и индивидуальных событиях объединены в систему - последовательную теорию бесконечных множеств.

Резиновый канат

А вот совсем новый парадокс, о котором не знал Зенон. На одном конце резинового каната находится червяк. Длина каната - 1 км.

Червяк ползет по канату с постоянной скоростью 1 см/с. Через 1 с после того, как червяк пустился в путь, канат растянули, и его длина стала равной 2 км. Через 2 с канат снова растянули, и его длина достигла 3 км. Каждую следующую секунду канат удлиняется на 1 км. Доползет ли червяк когда-нибудь до конца каната?

Ваша интуиция подсказывает вам, что червяк никогда не доползет до конца каната, но он все же доползет! Доползет-то доползет, но когда?

Задача легко решается, если учесть, что канат растягивается равномерно, как резиновая лента. Следовательно, при каждом растяжении червяк переезжает вперед - его переносит на себе, растягиваясь, сам канат.

Путь, пройденный червяком за каждую секунду, удобно выражать в долях длины каната к концу той же секунды. Как только сумма дробей, выражающих эти доли, станет равной 1, червяк достигнет конца каната.

В одном километре 100000 см, поэтому за первую секунду червяк преодолеет 1/100000 длины каната. За вторую секунду червяк проползет еще 1 см, что составляет 1/200000 от новой длины каната, которая достигнет уже 2 км. За третью секунду червяк проползает еще 1 см, что составляет 1/300000 от длины каната, которая к этому времени достигнет 3 км, и т. д. По истечении k секунд червяк проползет расстояние, составляющее от "текущей" длины каната долю, которая представима в виде

1/100000 (1/1 + 1/2 + 1/3 + 1/4 + … + 1/k).

В скобках стоит сумма первых k членов так называемого гармонического ряда. Заметим, что сумма членов, заключенных между 1/2 и 1/4, включая 1/4, то есть 1/3 + 1/4, больше, чем 2*1/4 = 1/2. Аналогично сумма членов, заключенных между 1/4 и 1/8, включая 1/8, то есть 1/5 + 1/6 + 1/7 + 1/8, больше, чем 4*1/8 = 1/2. Следовательно, сумма членов ряда, заключенных между 1/1 и 1/(2^k), включая 1/(2^k), всегда больше, чем k*1/2 = k/2, в чем нетрудно убедиться, если члены сгруппировать: возьмите сначала сумму двух первых членов, затем сумму следующих восьми членов и т.д. Частная сумма членов гармонического ряда может быть сделана сколь угодно большой.

Червяк доползет до конца каната, прежде чем с момента старта истекут 2(²⁰⁰⁰⁰⁰) с. Более точная оценка составляет e(¹⁰⁰⁰⁰⁰), где e - основание натуральных логарифмов (иррациональное число, чуть большее числа 2,7). Обе оценки дают представление о времени в пути (в с) и о пройденном червяком расстояния (в см).

Точная формула частичной суммы членов гармонического ряда приведена, например, в статье Р.П. Боаса и Дж.М. Ренча "Частичные суммы гармонического ряда" [American Mathematical Monthly, October 1971, 78, pp. 864-870]. Когда червяк доползет до конца, длина каната будет во много раз превышать диаметр известной части Вселенной. На свой нелегкий путь червяк затратит время, которое во много раз превышает возраст Вселенной по оценкам современной космологии. Разумеется, в задаче речь идет об "идеализированном" червяке и "идеализированном" канате - точке на прямой. Реальный червяк тихо скончался бы в самом начале путешествия, а реальный канат от растяжения стал бы таким тонким, что отдельные его молекулы оказались бы разделенными огромными пустыми промежутками.

Независимо от параметров задачи (начальной длины канала, скорости червяка, длины отрезка, на который увеличивается с каждой секундой длина каната) червяк всегда доползает до конца за конечное (хотя и очень большое) время. Интересные задачи возникают, если мы будем по-разному удлинять канат. Например, что произойдет, если длина каната будет возрастать в геометрической прогрессии, скажем удваиваться в каждую секунду? В этом случае червяк никогда не достигнет конца каната.

Сверхзадачи

Современные философы оживленно обсуждают новый класс парадоксов времени - так называемые сверхзадачи. В одном из простейших парадоксов этой серии речь идет о лампе. Нажимая на кнопку, ее можно включать и выключать

В течение 1 мин лампа включена, в течение следующей 1/2 мин - выключена, затем 1/4 мин лампа снова включена, после чего в течение 1/8 мин снова выключена и т. д. Вся серия включений и выключении длится ровно 2 мин. Будет ли лампа по истечении 2 мин включена или выключена?

Каждое нечетное нажатие кнопки включает лампу, каждое четное - выключает ее. Если по истечении 2 мин лампа включена, то это означает, что последнее число нечетное. Если же по истечении 2 мин лампа выключена, то последнее число четное. Но последнего натурального числа не существует. Лампа должна быть либо включена, либо выключена, но узнать, будет ли она включена или выключена, невозможно никаким способом!

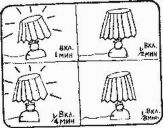
Парадоксы с "сверхзадачами", выполняемыми так называемыми "машинами бесконечности", и поныне волнуют специалистов по математической логике и философов. Парадокс с лампой известен под названием "лампа Томсона" - в честь впервые написавшего о нем Джеймса Ф. Томсона. Всякий согласится, что лампу Томсона нельзя построить реально, но дело не в этом. Главное в том, что если принять некоторые допущения, то лампа Томсона не приводит к логическим противоречиям. По мнению одних, лампа Томсона - вполне разумный "мысленный эксперимент", по мнению других, - вопиющая нелепость.

Парадокс с лампой Томсона беспокоит наш разум потому, что не существует логической причины, по которой лампу Томсона нельзя было бы бесконечно много раз включить и выключить. Если бегун Зенона успевает за 2 мин преодолеть бесконечно много отрезков дистанции, каждый из которых вдвое меньше предыдущего, то почему ровно за 2 мин нельзя успеть бесконечно много раз включить и выключить некую реально не существующую идеальную лампу? Но если лампа Томсона может за 2 мин бесконечно много раз перейти из состояния "вкл" в состояние "выкл", то это означает, что существует "последнее" натуральное число, с чем трудно согласиться.

Философ Макс Блэк сформулировал тот же парадокс несколько иначе. Он рассмотрел "машину бесконечности", переводящую шарик из лунки A в лунку B за 1 мин, затем возвращающую шарик из лунки B в лунку A за 1/2 мин, снова переводящую его из лунки A в лунку B за 1/4 мин и т.д., каждый раз вдвое быстрее, чем в предыдущий. Ряд 1 + 1/2 + 1/4 + … сходится, и все операции по перекатыванию шарика завершаются в течение 2 мин. Но в какой из лунок - в A или B - окажется шарик по истечении 2 мин? В какой бы из них он ни оказался, это будет означать что последнее натуральное число либо четно, либо нечетно. Так как последнего счетного числа не существует, то обе возможности, по-видимому, исключаются. Но если шарика нет ни в лунке A, ни в лунке B, то где же он?

Основные статьи по анализу "сверхзадач" опубликованы в сборнике "Парадоксы Зенона" под редакцией Весли Ч. Солмона. Подробному разбору такого рода парадоксов посвящена книга Адольфа Грюнбаума "Современная наука и парадоксы Зенона" [см. список литературы. - Перев.].

Мэри, Том и Фидо

Перед вами сверхзадача, выполненная собакой. В самом начале Фидо находится рядом с хозяином на расстоянии 1 км от Мэри.

Том и Мэри начинают сближаться со скоростью 2 км/ч каждый. Фидо, одинаково любящий хозяина и хозяйку, бегает от одного к другому и обратно со скоростью & км/ч. Добежав до хозяина и хозяйки, Фидо мгновенно поворачивается и пускается назад.

Путь Фидо представлен на графике в координатах время - расстояние. Куда будет обращена морда Фидо - к хозяину или к хозяйке, когда Том и Мэри встретятся посредине разделявшего их километрового отрезка?

На этот вопрос, так же как на вопрос о том, будет ли включена пли выключена по истечении бесконечной серии манипуляций с выключателем лампа Томсона, невозможно ответить. Но помочь Тому вычислить, какое расстояние пробежала собака, в наших силах. Том. Сколько пробежал Фидо? Но чтобы ответить на этот вопрос, мне нужно просуммировать длину бесконечно многих звеньев ломаной! Это очень трудная задача, Мэри!

Мэри. Совсем не трудная, милый! Мы идем со скоростью 2 км/ч. Значит, каждый из нас проходит полкилометра за 15 мин. Так как сначала нас разделяло расстояние 1 км, мы встречаемся через 15 мин.

Мэри. Фидо бегает со скоростью 8 км/ч. За четверть часа он пробегает 2 км. Вот и все. Том. Здорово! Мне даже не понадобился микрокалькулятор.

Предположим теперь, что Том, Мэри и Фидо находятся там, где они встретились. Том и Мэри идут той же дорогой с той же скоростью, но в обратном направлении, а Фидо бегает от одного из них к другому со скоростью 8 км/ч. Где будет Фидо, когда расстояние между Томом и Мэри снова станет равным 1 км?

Невероятно, но факт: Фидо не может находиться нигде между Томом и Мэри! Не верите? Убедитесь сами. Пусть вначале Фидо находится в любой точке километрового отрезка, разделяющего Тома и Мэри, которые начинают идти навстречу друг другу. Где бы ни находился Фидо, через 15 мин все трое сойдутся в центре отрезка.

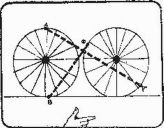
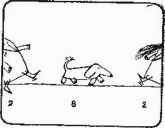
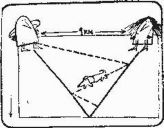
Первая задача (Том и Мэри идут навстречу друг другу, а Фидо бегает между ними туда и обратно) классическая. Она существует в различных вариантах. Иногда это задача о мухе, летающей туда и обратно между двумя сближающимися локомотивами, иногда - задача о птичке, порхающей между двумя едущими во встречных направлениях велосипедистами.

Рассказывают, что когда эту задачу предложили американскому математику Джону фон Нейману, тот сразу назвал правильный ответ. "Поздравляю! - сказал собеседник фон Неймана, сообщивший ему задачу. - Большинство людей пытаются решить задачу очень трудным способом, суммируя бесконечный ряд отрезков". "Но именно это я и сделал", - с удивлением ответил фон Нейман.

Итак, в какую сторону будет обращена морда Фидо в тот момент, когда Том и Мэри сойдутся посредине разделявшего их километрового отрезка? Задать такой вопрос все равно что спросить, будет ли включена или выключена лампа Томсона по окончании всех манипуляций с выключателем, или в какой из двух лунок, А или В, окажется в конце концов шарик. Это только кажется, будто Фидо должен быть обращен мордой либо к хозяину, либо к хозяйке. В действительности же любой ответ подразумевает, что существует последнее натуральное число (звеньев ломаной, по которой бежит собака), которое либо четно, либо нечетно.

Но если мы обратим процесс сближения Тома, Мэри и Фидо во времени, заставив Мэри и Тома расходиться из середины километрового отрезка, а Фидо по-прежнему бегать между хозяином и хозяйкой, то возникнет новый парадокс. Наша интуиция подсказывает нам, что если некую однозначно определенную процедуру обратить во времени, то есть изменить направление всех движений на противоположное, то мы должны вернуться к тому, с чего начали. Однако в рассматриваемом случае процедура при обращении времени утрачивает однозначную определенность. Если события развиваются от начала к концу, то Фидо оказывается в середине километрового отрезка, разделявшего Тома и Мэри. Но если события развиваются от конца к началу, то место, где будет находиться Фидо, когда Том и Мэри разойдутся на 1 км, невозможно указать однозначно: пес может находиться в любой точке отрезка.

Более подробный анализ этого парадокса проведен Весли Солмоном (Scientific American, декабрь 1971). И задача о двух хозяевах и их верной собаке, и парадоксы Зенона, и лампа Томсона могут служить описательным введением в теорию пределов и суммирования бесконечной геометрической прогрессии.

Ломаная, по которой бежит Фидо, похожа на траекторию прыгающего мячика. Вот несложная задача о таком мячике. Предположим, что круглый мяч брошен на пол с высоты 1 м. Высота, на которую подпрыгивает мяч, каждый раз вдвое меньше предыдущей. Если каждый подскок длился бы 1 с, то мяч прыгал бы вечно. Но как и в парадоксах с бегуном Зенона, машиной, перемещающей шарик из лунки в лунку, и Фидо, на прохождение каждого следующего отрезка траектории требуется меньше времени, чем на прохождение предыдущего. Очередной подскок занимает 1/2 от продолжительности предыдущего подскока. Последовательность времен сходится. Следовательно, по истечении конечного промежутка времени мяч остановится, хотя теоретически он подпрыгнет бесконечно много раз. Суммарная высота всех подскоков составит 1 + 1/2 + 1/3 + … + 1/n = 2 м.

Предположим, что мяч подпрыгивает каждый раз на высоту, составляющую 1/3 от предыдущей. Какова суммарная высота всех подскоков в этом случае?

• 1
• 2

• целиком
• следующая →