Геометрия
Парадоксы о плоскости, пространстве и невозможных формах
Большинство людей понимает под геометрией евклидову геометрию на плоскости, то есть изучение свойств жестких плоских фигур. В этой главе мы будем понимать геометрию в более широком смысле - так, как ее определил более века назад Феликс Клейн. Геометрия, по Клейну, занимается изучением свойств фигур в пространстве любого числа измерений, остающихся неизменными, или инвариантными, относительно любой заданной группы преобразований. Предложенная Клейном концепция геометрии оказалась наиболее плодотворной для унификации понятий в современной математике. В евклидовой планиметрии и стереометрии допустимые преобразования состоят из трансляций (перемещений с одного места на другое), зеркальных отражений, поворотов и сжатий или растяжений. Более глубокие преобразования приводят к аффинной геометрии, проективной геометрии, топологии и, наконец, теории множеств, в которой фигуру разрешается "рассыпать" на отдельные точки, с тем чтобы составить из них новую фигуру.
Швейцарский психолог Жан Пиаже считает, что дети постигают геометрические свойства в обратном порядке. Например, малышу легче понять различие между кучкой красных и кучкой синих шариков (теория множеств) или между замкнутой в кольцо и разомкнутой резиновой лентой (топология), чем отличить пятиугольник от шестиугольника (евклидова геометрия).
Топология - довольно необычный раздел геометрии, изучающая свойства фигур, инвариантные относительно непрерывных деформаций. Представьте себе, что фигура или тело изготовлены из резины. Вы можете как угодно изгибать, растягивать и сжимать ее. Запрещается только отрывать часта и приклеивать их. Например, лист Мёбиуса обладает таким топологическим свойством, как односторонность: если представить его сделанным из резины, то как бы вы ни изгибали и ни растягивали его, он все равно останется односторонним. Многие собранные в этой главе парадоксы связаны с топологическими свойствами.
Преобразованиям отражения, переводящим асимметричные фигуры, например прописную букву Л, в их зеркальные отражения, мы уделяем внимание не только потому, что с отражениями связано много парадоксов, но и потому, что они играют важную роль в современной геометрии и естественных науках. Зеркальная симметрия играет фундаментальную роль в химии, особенно органической, в которой большинство соединений существует в двух формах (левой и правой), в кристаллографии, биологии (в частности, в генетике) и в физике элементарных частиц.
Хотя некоторые из собранных в этой главе парадоксов могут показаться забавными безделушками, каждый из них, как вы вскоре убедитесь, довольно быстро и незаметно приводит к таким важным разделам математики, как теория групп, математическая логика, теория бесконечных последовательностей, рядов и пределов. Те, кто изучает геометрию, обычно уделяют так много внимания построениям с помощью циркуля и линейки и доказательству сложных теорем, что совершенно упускают из виду связи, существующие между геометрией и другими областями математики, не говоря уже о нескончаемых и прекрасных приложениях, которые геометрия находит в астрономии, физике и других науках.
Вокруг да около
Этот старинный парадокс многие знают как историю о белке и охотнике. Белка сидит на дереве. Охотник, пытаясь подкрасться к ней сзади, обходит вокруг дерева, но зверек, не спуская глаз с охотника, прячется за стволом и постепенно описывает полный круг. Обойдет ли охотник вокруг белки после того, как он обойдет вокруг дерева?
Разумеется, на этот вопрос невозможно ответить, пока мы не условимся, в каком смысле надлежит понимать слово "вокруг". Многие слова в повседневной речи не имеют точных определений. Остроумный разбор парадокса с охотником и белкой дан в классическом философском сочинении Уильяма Джеймса "Прагматизм". Джеймс приводит этот парадокс как модель чисто семантического разногласия. Трудности такого рода исчезают, как только обе стороны осознают, что спор по существу идет об определении слова. Если бы люди отдавали себе ясный отчет в важности точных определений того или иного слова, многие ожесточенные споры разрешались бы почти столь же безболезненно.
Загадка Луны
Этот парадокс, как и предыдущий, по существу сводится к семантической проблеме: в каком смысле понимать выражение "вращается вокруг своей оси"? Относительно наблюдателя, находящегося на Земле, Луна не вращается вокруг свой оси. Относительно наблюдателя, находящегося за пределами системы Земля - Луна, наш естественный спутник вращается вокруг оси.
Трудно поверить, но даже люди, известные своей ученостью, относились к этому парадоксу весьма серьезно. Август Де Морган в первом томе своей книги "Кладезь парадоксов" дал обстоятельный обзор нескольких брошюр XIX в., подвергавших резкой критике тезис о том, что Луна вращается вокруг собственной оси. Лондонский астроном-любитель Генри Перигэл был неистощим на аргументы, опровергавшие вращение Луны. По словам автора посвященного ему некролога, "главной астрономической целью жизни" Перигэла было убедить всех в том, что Луна не вращается вокруг своей оси. Перигэл писал брошюры, строил модели и даже сочинял поэмы, чтобы опровергнуть широко распространенное убеждение в том, будто Луна вращается, "стойко перенося непрерывное разочарование при виде того, как ни один из его аргументов не достигает цели".
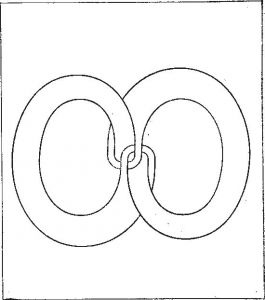
В связи с парадоксом о вращении Луны нельзя не упомянуть об одной замечательной геометрической задачке. Начертите два соприкасающихся круга одного и того же радиуса. Представьте себе, что это два диска. Будем обкатывать один диск вокруг другого так, чтобы он не проскальзывал и ободы дисков все время соприкасались. Сколько раз повернется катящийся диск вокруг своей оси, пока совершит полный оборот вокруг неподвижного диска?
Большинству людей кажется, что катящийся диск повернется вокруг своей оси один раз. Предложите им проверить свой ответ на двух монетах одного и того же размера. К своему удивлению, они обнаружат, что за один оборот вокруг неподвижной монеты катящаяся монета успевает дважды повернуться вокруг своей оси!
Но … вращается ли катящаяся монета? Как и в парадоксе с Луной и Землей, ответ на этот вопрос зависит от системы отсчета наблюдателя. Относительно начальной точки касания с неподвижной монетой катящаяся монета совершает один оборот. Относительно вас, наблюдателя, глядящего на монеты со стороны, катящаяся монета за один оборот вокруг неподвижной монеты поворачивается дважды. Когда задача о монетах была впервые опубликована в журнале Scientific American за 1867г., в редакцию хлынул поток негодующих писем от читателей, придерживавшихся противоположного мнения.
Читатели довольно быстро установили связь между парадоксом с монетами и парадоксом с Луной и Землей. Те, кто считал, что катящаяся монета успевает за один оборот вокруг неподвижной монеты лишь один раз повернуться вокруг собственной оси, склонялись к мнению, что Луна не вращается вокруг собственной осп. "Станут ли вращаться вокруг собственных осей голова, глаза и позвонки кошки, - вопрошал один из читателей, - которую вы крутите за хвост у себя над головой?.. Разве несчастное животное не погибло бы на девятом обороте?"
Редакционная почта достигла столь угрожающих размеров, что в апреле 1868г. редакторы объявили о прекращении дискуссии на страницах журнала Scientific American и о продолжении ее на страницах нового журнала The Wheel ("Колесо"), специально посвященного "великой проблеме". По крайней мере один номер журнала вышел. Основное место среди иллюстраций там занимают многочисленные схемы и рисунки сложных устройств, призванных, по замыслу приславших их читателей, убедить редакторов в ошибочности занятой ими позиции.
Вращение небесных тел порождает различные эффекты, которые можно обнаружить с помощью таких устройств, как маятник Фуко. Если такой маятник поместить на Луне, то окажется, что, совершая обороты вокруг Земли, Луна вращается вокруг своей оси. Можно ли считать эти физические соображения аргументом, подтверждающим вращение Луны вокруг собственной оси независимо от системы отсчета наблюдателя?
Как ни удивительно, но в свете общей теории относительности ответ на этот вопрос должен быть отрицательным. Вы можете считать, что Луна вообще не вращается, а вся Вселенная (независимо от того, зависит или не зависит ее пространственно-временная структура от распределения материи) вращается вокруг Луны. Вращающаяся Вселенная создает такие же гравитационные поля, как и Луна, вращающаяся в неподвижном космосе. Разумеется, за неподвижную систему отсчета все же удобнее принимать Вселенную. Но, строго говоря, вопрос о том, "действительно" ли вращается или покоится любой объект, в теории относительности не имеет смысла. "Реально" лишь относительное движение.
Волшебное зеркало
Поскольку каждая буква слова ТОМ обладает вертикальной осью симметрии, его зеркальное отражение совпадает с оригиналом. В слове РЕБЕКА вертикальной осью симметрии обладает только буква А. Поэтому при отражении в зеркале только она переходит в себя, а остальные буквы - в зеркальные отражения, отличные от их исходных начертаний.
Почему зеркало меняет местами правую и левую стороны, но оставляет на месте верх и низ? Подобно парадоксу с Луной и Землей, этот парадокс приводит к вопросу, на который невозможно ответить, не условившись предварительно относительно значений таких слов, как "левое", "правое", "менять местами". [Более подробный анализ того, что происходит при отражении в зеркале см. в книге: Гарднер М. Этот правый, левый мир. - М.: Мир, 1967. Там же вы сможете почерпнуть обширные сведения о зеркальной симметрии и ее роли в естественных науках и повседневной жизни. - Пер.]
Буквы в слове КОФЕ обладают горизонтальной осью симметрии (в некоторых типографских гарнитурах симметрия относительно горизонтальной оси может незначительно нарушаться). Следовательно, если к слову КОФЕ приставить зеркало сверху (или снизу), то буквы К, О, Ф и Е при отражении перейдут в себя. В слове ЧАЙ буквы не обладают симметрией относительно горизонтальной оси, поэтому при отражении в приставленном сверху зеркале они переходят в знаки, отличные от букв Ч, А и И.
Какие еще слова не изменяются при отражении в зеркале, приставленном к ним сверху? Для того чтобы ответить на этот вопрос, необходимо перебрать все прописные буквы русского алфавита и отобрать из них те, которые обладают горизонтальной осью симметрии: В, Е, Ж, 3, К, Н, О, С, Ф, X, Э (в зависимости от типографской гарнитуры симметрия букв может несколько нарушаться). Из них можно составить слова, переходящие в себя при отражении в зеркале, приставленном сверху или снизу, например ЭХО, НОС, ФОН, СНЕЖОК и др.
Необращенное изображение своего лица вы можете увидеть, взглянув в два карманных зеркальца, составленных под прямым углом. (Вертикальная ось симметрии вашего лица должна лежать в плоскости, делящей пополам угол между зеркалами. Составив зеркала, пошевеливайте ими: если угол раствора прямой, вы должны видеть полное отражение своего лица.) Если вы подмигнете левым глазом, то ваше зеркальное отражение подмигнет вам глазом, расположенным против вашего правого, а не левого глаза, как можно было бы ожидать. Обе половины вашего лица отражены дважды - каждым из двух зеркал.
Возможно, собственное лицо покажется вам незнакомым. Глядя в обычное зеркало, вы всегда видите отражение своего лица, у которого правая и левая половины переставлены. Хотя лицо обладает вертикальной осью симметрии, правая и левая половины редко бывают полностью зеркально-симметричными. Когда вы видите свое необращенное лицо, небольшие различия между его правой и левой половинами делают его непривычным, хотя указать, что именно кажется странным бывает довольно трудно. И все же именно так вы выглядите в глазах всего мира! Более того, привычное вам зеркальное отражение вашего лица кажется странным для тех, кто видит вас без зеркала.
Существует хороший способ проверить, насколько вы разобрались в механизме действия двойного зеркала: спросите себя, что вы увидите, взглянув в два зеркала, составленные под прямым углом так, чтобы ребро образуемого ими двугранного угла заняло горизонтальное положение? Двукратное отражение 8 таком зеркале окажется перевернутым! Является ли перевернутое изображение вашего лица еще и обращенным? Нет, перевернутое отражение, как и прямое, не обращено. Стоит вам подмигнуть левым глазом, как вы увидите, что лицо в зеркале подмигнет вам глазом, расположенным против вашего правого глаза.
Все эти фокусы с зеркалами служат великолепным введением в теорию симметрии и отражений в курсе геометрических преобразований. Элементарная теория преобразований позволяет объяснить все парадоксы, связанные с зеркальной симметрией.
Кубики и прекрасная незнакомка
Все эти оптические иллюзии - примеры того, как один и тот же рисунок может по-разному восприниматься нашим сознанием. В первом случае ваш разум воспринимает плоский рисунок как перспективное изображение сложенной из кубиков пирамиды, причем рисунок допускает две интерпретации. Они обе одинаково допустимы, и наш разум колеблется между ними, будучи не в силах отдать предпочтение ни одной из них.
То же можно сказать и о портрете то ли прекрасной молодой девушки, то ли безобразной старухи. Невозможно видеть что-нибудь одно: наш разум непрестанно мечется от одной интерпретации к другой.
Третья оптическая иллюзия допускает сразу три интерпретации. Для большинства людей труднее всего увидеть блок с кубической выемкой, поскольку такие выемки встречаются сравнительно редко. Но если вы, глядя на рисунок, попытаетесь представить себе, что перед вами блок, из которого вырезан кубик, то сможете увидеть выемку. Обучение "видению" трех возможных интерпретаций последнего рисунка тесно связано с вашей способностью интерпретировать геометрические чертежи. В геометрии неверное "видение" чертежа - один из основных источников ошибок.
Мистер Рэнди и его необыкновенные ковры
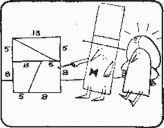
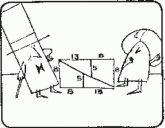
Этот классический парадокс настолько поразителен и труднообъясним, что вы не пожалеете, если перечертите выкройку мистера Рэнди на бумаге в клеточку и, разрезав ее на части, составите из них прямоугольник. Если части прямоугольника не очень велики и вырезаны и вычерчены с обычной, не слишком высокой точностью, то вы вряд ли заметите, что вдоль главной диагонали прямоугольника эти части слегка перекрывают одна другую. Именно тем, что части не прилегают друг к другу, а находят друг на друга вдоль главной диагонали, и объясняется таинственное исчезновение 1 дм2. Если ссылка на перекрытие частей покажется вам недостаточно убедительной, вы легко сможете проверить ее правильность, сравнив угол наклона диагонали прямоугольника и угол наклона соответствующих участков периметра четырех частей.
А что, если начертить на листе в клеточку прямоугольник и, разрезав его на части, составить из них квадрат? Это тоже интересная задача, и, возможно, вам захочется решить ее.
Длины отрезков, фигурирующих в этом парадоксе, равны 5, 8, 13 и 21 дм. Возможно, вы вспомните, что уже встречали эти числа как члены знаменитой последовательности. А может быть, вы вспомните и рекуррентное соотношение, которому удовлетворяют ее члены? Они называются числами Фибоначчи. Каждое из них равно сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34…
Другие варианты того же парадокса основаны на использовании других четверок последовательных чисел Фибоначчи. Но о каком бы из вариантов ни шла речь, площадь прямоугольника неизменно отличается от площади квадрата: в одних случаях на 1 больше, в других - на 1 меньше. Далее вы обнаружите, что когда площадь прямоугольника на 1 меньше, то вдоль его главной диагонали части перекрываются, образуя едва заметный ромб площадью как раз в недостающую единицу, а когда площадь прямоугольника на 1 больше, то вдоль главной диагонали части не примыкают друг к другу вплотную, оставляя зазор в форме ромба площадью в лишнюю единицу.
Можно ли, зная, какие именно четыре последовательных числа Фибоначчи положены в основу варианта, предсказать, будет ли площадь прямоугольника больше или меньше площади квадрата? Оказывается, можно. Парадокс наглядно демонстрирует одно из фундаментальных свойств чисел Фибоначчи: квадрат любого числа Фибоначчи равен произведению двух соседних (предшествующего и последующего) чисел плюс или минус 1, то есть
Fn2 = Fn-1Fn+1 +/- 1.
Левая часть этого равенства задает площадь квадрата со стороной Fn, а правая - уменьшенную или увеличенную на 1 площадь прямоугольника со сторонами Fn-1 и Fn+1. Знаки "плюс" и "минус" чередуются при переходе от одного числа Фибоначчи к следующему. Квадраты чисел Фибоначчи с нечетными номерами (например, 2, 5, 13) на 1 больше произведения двух соседних чисел с четными номерами. Квадраты чисел Фибоначчи с четными номерами (например, 3, 8, 21) на 1 меньше произведения двух соседних чисел с нечетными номерами. Зная, это, вы легко можете предсказать, будет ли прямоугольник, составленный из частей квадрата, больше или меньше квадрата.
Последовательность "настоящих" чисел Фибоначчи начинается с двух единиц, но последовательность "обобщенных" чисел Фибоначчи может начинаться с любых двух чисел. Вы можете рассмотреть варианты парадокса, основанные на обобщенных числах Фибоначчи. Например, последовательность 2, 4, 6, 10, 16, 26, … порождает прямоугольники, площадь которых отличается то в одну, то в другую сторону от площади квадрата на 4. Последовательность 3, 4, 7, 11, 18, … порождает прямоугольники, площадь которых отличается то в одну, то в другую сторону от площади квадрата на 5.
Пусть a, b и c - любые три последовательных обобщенных числа Фибоначчи, а x - разность площадей прямоугольника и квадрата (избыток или недостаток) . Тогда справедливы две формулы:
a + b = c,
b2 = ac +/- x.
Подставив вместо x любой избыток или недостаток площади, а вместо b - любую длину стороны квадрата и решив систему двух выписанных выше уравнений, мы найдем соответствующие значения a и c (хотя они не обязательно получатся рациональными) .
А нельзя ли разрезать квадрат на четыре части так, чтобы из них можно было составить прямоугольник, площадь которого была бы равна площади квадрата?
Чтобы ответить на этот вопрос, положим во втором из уравнений нашей системы x = 0 и выразим b через a. Единственное положительное решение (отрицательное мы отбрасываем, так как Ь - длинa отрезка) имеет вид
b = (1 + sqrt(5)) a/2.
Величина (1 + sqrt(5))/2 - знаменитое золотое сечение, или phi. Это иррациональное число, равное 1,618033…. Иначе говоря, числа
1, phi, phi2, phi3, phi4, …
образуют единственную последовательность Фибоначчи, обладающую тем свойством, что квадрат любого ее члена (начиная со второго) равен произведению двух соседних членов.
После некоторых преобразований можно показать, что последовательность Фибоначчи эквивалентна последовательности
1, phi, phi+1, 2phi+1, 3phi+2, … (*)
и ее члены обладают отличительным признаком чисел Фибоначчи: каждый из них (начиная с третьего) равен сумме двух предыдущих.
Только разрезая квадрат на части, длины которых совпадают с четверками последовательных чисел Фибоначчи из (*), мы получим вариант парадокса с равновеликими прямоугольником и квадратом. Более подробно о золотом сечении и о его связи с парадоксом о разрезании квадрата и превращении его в прямоугольник см. в главе 23 ("Число phi - золотое сечение") моей книги "Математические головоломки и развлечения" [Гарднер М. Математические головоломки и развлечения. М.: Мир, 1971, с.125-132.].
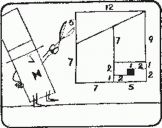
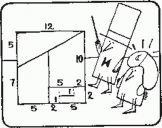
Могут ли два одинаковых квадрата иметь различную площадь? Во втором парадоксе с коврами мистера Рэнди недостающая площадь имеет правдоподобное объяснение: это дырка, прожженная в ковре. В отличие от предыдущего парадокса все части примыкают без зазоров, и ни одна часть не перекрывает другую. Куда же исчезает недостающий квадрат со стороной 1?
Чтобы ответить на этот вопрос, приготовим два экземпляра квадрата без дыры. Чем больше получатся квадраты, тем лучше. Один квадрат аккуратно разрежем на части по выкройке, составим из них квадрат с дырой и наложим на него второй квадрат. Если верхний край и боковые стороны обоих квадратов совпадают, то вы легко заметите, что второй "квадрат" - вовсе не квадрат, а прямоугольник, который выше квадрата на 1/12 дм. Площадь полоски 12x1/12 дм2, выступающей за пределы квадрата, равна площади "бесследно" исчезнувшей дыры.
Итак, недостающий единичный квадрат найден! Но отчего вытянулся в высоту "квадрат"? От того, что вершина, которая расположена на гипотенузе части, имеющей форму прямоугольника, не совпадает с узлом квадратной решетки, па которую разграфлена бумага. Зная это, вы сможете построить варианты этого парадокса, в которых избыток или недостаток площади больше 1.
Описанный парадокс известен под названием "квадрат Керри" (фокусника-любителя из Нью-Йорка, открывшего основной принцип подобных парадоксов) и существует во множестве вариантов, включающих не только квадраты, но и треугольники. Тем, кто захочет побольше узнать о квадратах и треугольниках, рекомендую обратиться к моим книгам "Математические чудеса и тайны" [Гарднер М. Математические чудеса и тайны. М.: Наука, 1964, с.84-102.] и "Математические головоломки и развлечения" [Гарднер М. Математические головоломки и развлечения. М.: Мир, 1971, с.125-132.].